Biliard_Torus
Unfolding the Billiard
Introduzione
È stata sviluppata una simulazione volta a mostrare i risultati ottenuti nel paper “Trajectory tracking in rectangular billiards by unfolding the billiard table”. In particolare, il moto di una pallina all’interno di un biliardo, con pareti elastiche, può essere mappato sulla superficie di un toroide.
Tavolo del Biliardo
Innanzitutto, mediante l’uso di Matplot Lib, una libreria di Python, vengono tracciate delle linee di riferimento che individuano il perimetro di un quadrilatero di lati b e h. Tale oggetto rappresenta il “campo da gioco” della simulazione ossia il biliardo. Successivamente, si definiscono le coordinate di un punto detto spawn point, il quale giace all’interno del biliardo definito precedentemente, che costituisce il punto di partenza della simulazione, di fatto una pallina.
Il moto della pallina è costruito analiticamente: si fissa una direzione arbitraria e si traccia una retta che ne indica la traiettoria. È chiaro che, durante il moto, la pallina urterà le pareti del biliardo. Per rendere più semplice il nostro lavoro è stato implementato l’effetto pac-man sulle pareti. Per l’equivalenza dei due fenomeni di veda l’immagine seguente.
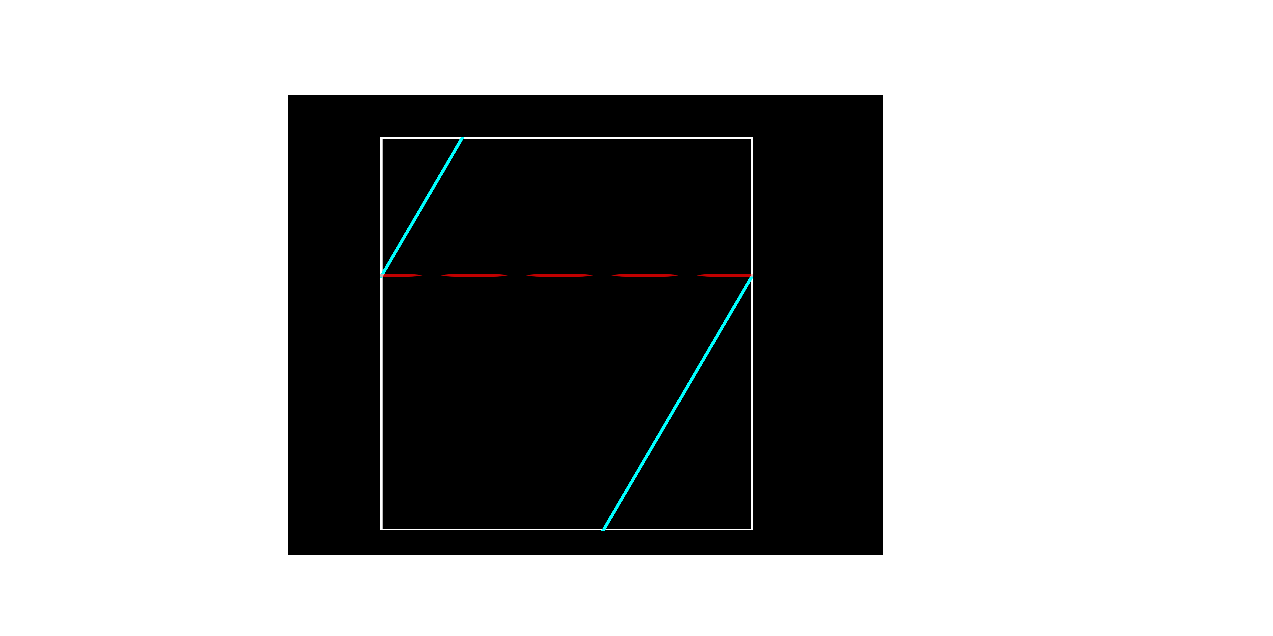
La pallina sbuca fuori dalla parte opposta, senza variare la sua direzione.
Costruzione delle traiettorie
A partire dalla prima traiettoria vengono tracciate le successive sulla base della seguente logica:
Tale logica implementa l’effetto pac-man: il punto d’intersezione con la parete del biliardo viene traslato dalla parte opposta per disegnare la nuova traiettoria. La pendenza non viene cambiata mentre, tramite la formula inversa della retta si ricava l’intercetta.
È importante notare che nel nostro algoritmo l’angolo d’incidenza traiettoria-parete, rispetto alla normale della parete stessa, non può essere pari a \(\frac{\pi}{2}\). Il motivo è che la pendenza di una retta è pari alla tangente dell’angolo che essa forma con l’asse delle ascisse
\[m = {tg}(\alpha)\]Ricordando il dominio della funzione tangente risulta chiaro che l’angolo di incidenza non può essere mai pari a \(\frac{\pi}{2}\) . Inoltre, si precisa che: nel caso in cui la pallina urti perfettamente uno degli spigoli del biliardo, le traiettorie sarebbero tutte sovrapposte e quindi di poco d’interesse.
Traiettorie Dense
Innanzitutto si osservi l’animazione riportata di seguito:

Si nota che a partire da un segmento, unendo le due estremità, si giunge ad una circonferenza. Si passa poi ad un Toroide facendo ruotare la circonferenza attorno ad un asse e preservandone la traccia durante il suo moto (colorata in arcobaleno).
Tale animazione è intesa come strumento esemplificativo per comprendere che le considerazioni relative al caso unidimensionale possono essere estese al caso tridimensionale.
Si consideri dunque la funzione:
\[\ \ T_{\theta}:\lbrack 0,1) \rightarrow \lbrack 0,1)\ con\ \theta \mathbb{\in R}.\] \[\\ \ \ \ x \mapsto \{x + \theta\}\]Dove \(\{x + \theta\}\) indica la parte frazionaria. Per semplicità si considera un segmento di lunghezza unitaria e si fissa un punto di partenza \(x \in \lbrack 0,1)\) Definiamo:
\[T_{\theta}^{0}(x) = x\] \[T_{\theta}^{1}(x) = T_{\theta}(x)\] \[T_{\theta}^{2}(x) = T_{\theta}( T_{\theta}(x) )\] \[T_{\theta}^{n} = \underbrace{(T_{\theta} \circ T_{\theta} \circ \cdots \circ T_{\theta})}_{n \text{ volte}}(x)\]Lemma 1
Si ha \(T_{\theta}^{n}(x) = \{ x + n\theta \}\) per ogni \(n\mathbb{\in N}\). Si dimostra per induzione.
Per \(n = 0\), si ha per definizione che:
\[T_{\theta}^{0}(x) = x = \{x + \theta\}\]Assumiamo sia:
\[T_{\theta}^{n}(x) = \{ x + n\theta \}\]Si applica \(T_{\theta}\) ambo i membri:
\[T_{\theta} \circ T_{\theta}^{n}(x) = T_{\theta}( \{ x + n\theta \} )\] \[T_{\theta}^{n + 1}(x) = \{ \{ x + n\theta \} + \theta \}\] \[= \{ (x + n\theta) - \lbrack x + n\theta\rbrack + \theta \}\] \[= \{ x + (n + 1)\theta - \lbrack x + n\theta\rbrack \}\] \[= \{ x + (n + 1)\theta - \lbrack x + n\theta\rbrack - \lbrack x + (n + 1)\theta - \lbrack x + n\theta\rbrack \rbrack \}\] \[= x + (n + 1)\theta - \lbrack x + n\theta\rbrack - \lbrack x + (n + 1)\theta \rbrack + \lbrack x + n\theta\rbrack\] \[= \{ x + (n + 1)\theta \}\]◻
Si definisce poil’immagine della successione \(\{ T_{\theta}^{n}(x) \}_{n}\) , cioè l’insieme \(\tau(x) = \{ T_{\theta}^{n}(x):n\mathbb{\in N} \}\). Vale che \(\tau(x) \subseteq \lbrack 0,1)\).
Teorema 1
La successione \(\{ T_{\theta}^{n}(x) \}_{n}\) è periodica \(\Leftrightarrow \theta \mathbb{\in Q}\).
DIM:
Se la successione è periodica, allora esiste un \(N\mathbb{\in N}\) tale che:
\[T_{\theta}^{0}(x) = x = T_{\theta}^{N}(x) = x + N\theta - \lbrack x + N\theta\rbrack\]Da cui:
\[\theta = \frac{\lbrack x + N\theta\rbrack}{N}\]Essendo \(\theta\) dato dal rapporto di due numeri interi, allora è un numero razionale. Nell’altra direzione, se si suppone \(\theta\mathbb{\in Q}\), allora
\(\theta = \frac{N}{M}\mathbb{\in Q}\) con \(N,M\in\mathbb{Z}, e\, M\neq 0\)
Per \(\theta = 0\), si ha il caso base della definizione ed il teorema è chiaramente verificato. Per gli altri casi basta trovare anche un solo esempio in cui si nota la periodicità. Al passo \(M\) si avrà:
\[T_{\theta}^{M}(x) = \{ x + M\theta \} = \{ x + M\frac{N}{M} \} = \{ x + N \} = \{ x \} = x = T_{\theta}^{0}(x).\]◻
Lemma 2
Su \(\lbrack 0,1)\) si definisce la distanza tra due punti \(x,y\), la quantità:
\[\mathbb{d}(x,y) = min(\{ |x - y|,|x - y + 1|,|x - y - 1| \})\]Possiamo mostrare che:
\[\mathbb{d}(x,y) = \mathbb{d}( T_{\theta}^{n}(x), T_{\theta}^{n}(y) )\]
Quando a partire dal segmento si giunge alla circonferenza, si hanno due modi per collegare due punti: si formano due archi. La distanza è data quindi dall’arco di lunghezza minima. La facoltà di scegliere il percorso minore è contemplata quando si considera l’offset di \(\pm 1\) a seconda dei casi.
Teorema 2
Le seguenti tre proposizioni sono equivalneti: (i) La successione \(\{ T_{\theta}^{n}(x) \}_{n}\) non è periodica (ii) \(\theta\mathbb{\in R \smallsetminus Q}\) (iii) L’immagine \(\tau(x)\) è densa in \(\lbrack 0,1)\).
DIM: L’equivalenza di (i) e (ii) viene dal lemma. Per mostrare che (iii) implica (i) e (ii) basta notare che se \(\{ T_{\theta}^{n}(x) \}_{n}\) è periodica, allora \(\tau(x)\) è finito e non può essere denso. Rimane da dimostrare che (ii) (oppure (i)) implica (iii). Facciamo la dimostrazione in due passi.
- Si verifica innanzitutto che gli elementi di \(T_{\theta}^{n}(x)\) sono tutti diversi.
Se così non fosse sarebbe:
\(T_{\theta}^{n}(x) = T_{\theta}^{m}(x)\)per qualche \(n,m\mathbb{\in N}\)
\[\{ x + n\theta \} = \{ x + m\theta \}\] \[x + n\theta - \lbrack x + n\theta\rbrack = x + m\theta - \lbrack x + m\theta\rbrack\] \[\theta = \frac{\lbrack x + n\theta\rbrack - \lbrack x + m\theta\rbrack}{n - m}\]In questo caso \(\theta\) è dato dal rapporto di due numeri interi per cui \(\theta\mathbb{\in Q}\). Ma si era detto che \(\theta \in \mathbb{R \smallsetminus Q}\). Quindi gli elementi della successione sono tutti diversi \(\theta\mathbb{\in R \smallsetminus Q}\).
- Si verifica adesso che l’immagine \(\tau(x)\) è densa in \(\lbrack 0,1)\).
Si divida il segmento unitario, in cui è definita la successione, in \(N\) intervallini di lunghezza \(\frac{1}{N}\). Se si considera il fatto che la successione parte dal passo \(T_{\theta}^{0}(x)\) ed arriva al paso \(T_{\theta}^{N}(x)\), allora saranno generati \(N + 1\) numeri. Affinché questi stiano all’interno della precedente suddivisione, deve essere che almeno un intervallino ne contenga almeno due. Siano questi:
\[T_{\theta}^{n_{0}}(x) \quad \text{e} \quad T_{\theta}^{m_{0}}(x) \quad \text{con} \quad n_{0}, m_{0} \in \{0, 1, 2, \ldots, N\}\]Vale quindi che:
\[| T_{\theta}^{n_{0}}(x)\ - \ T_{\theta}^{m_{0}}(x) | < \frac{1}{N}\]e quindi
\[\mathbb{d}( \ T_{\theta}^{m_{0}}(x),\ T_{\theta}^{n_{0}}(x) ) < \frac{1}{N}.\]Si applica \(T_{\theta}^{- m_{0}}\) (con \(n_{0} > m_{0}\)) e ricordando il Lemma 2 si ottiene:
\[\mathbb{d}(T_{\theta}^{-m_0}(x) \circ T_{\theta}^{m_0}(x), T_{\theta}^{-m_0} \circ T_{\theta}^{n_0}(x)) < \frac{1}{N}\] \[\mathbb{d}( x,T_{\theta}^{n_{0} - m_{0}}(x) ) < \frac{1}{N}\]Si consideri ora la successione:
\[\{x_{j}\}_{j} = \{T_{\theta}^{j(n_{0} - m_{0})}(x)\}\]Si nota che questa è una sotto-successione di \(\{ {T_{\theta}^{n}}(x) \}_{n}.\)
Si applichi ora il Lemma 2 tra due punti della sotto-successione:
\[\mathbb{d}( T_{\theta}^{j( n_{0} - m_{0} )}(x),T_{\theta}^{(j + 1)( n_{0} - m_{0} )}(x) )\] \[= \mathbb{d}( T_{\theta}^{j( n_{0} - m_{0} )}(x),T_{\theta}^{j( n_{0} - m_{0} )}( T_{\theta}^{n_{0} - m_{0}}(x) ) )\] \[= \mathbb{d}( x,T_{\theta}^{n_{0} - m_{0}}(x) ) < \frac{1}{N}\]Quindi si è ottenuta una sotto-successione che ha un passo più breve di \(\frac{1}{N}\). Poiché è possibile scegliere \(N\) grande quanto si vuole, allora anche il passo può essere piccolo quanto si vuole.
Concludiamo che \(\tau(x)\) è densa in \(\lbrack 0,1)\).
Mappatura sul Toroide
Un Toroide può essere definito mediante le seguenti equazioni parametriche:
\[\begin{cases} x(\omega, \varphi) = (R + r \cos(\omega)) \cos(\varphi) \\ y(\omega, \varphi) = (R + r \cos(\omega)) \sin(\varphi) \\ z(\omega, \varphi) = r \sin(\omega) \end{cases} \quad \text{con } \omega, \varphi \in [0, 2\pi)\]Dove \(\omega\), φ sono gli angoli di rotazione, r è il raggio del tubo del Toroide, R è la distanza dal centro del tubo al centro di rotazione del Toroide.
Il motivo per il quale si giunge al Toroide è dato dalla seguente animazione esemplificativa:

È possibile ottenere un Toroide a partire da un rettangolo se si incollano tra di loro il bordo superiore e inferiore e poi quello destro e sinistro
Ricordando che la traiettoria della pallina è costruita mediante rette, e che queste vengono disegnate operativamente unendo dei punti tra di loro, è possibile sfruttare tali punti per mappare una traiettoria curvilinea sul Toroide. Passando quindi da un grafico in 2D ad uno tridimensionale mediante le seguenti proporzioni:
\[\begin{cases} \theta : 2\pi = x : b \\ \varphi : 2\pi = y : h \\ \end{cases}\] \[\begin{cases} \theta = \frac{2\pi \cdot x}{b} \\ \varphi = \frac{2\pi \cdot y}{h} \end{cases}\]Dove b e h sono rispettivamente la base e l’altezza del rettangolo. Infine sfruttando le coordinate parametriche di prima si costruisce il Toroide.
Traiettorie dense nel toroide
Si consideri un punto \(( x_{0},y_{0} ) \in \lbrack 0,1)^{2}\) e due numeri \(\alpha, \beta \in \mathbb{R} \setminus \{0\}\).
Quindi si definisce la mappa:
\[\phi\mathbb{:R \rightarrow}\lbrack 0,1)^{2}\] \[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ t \mapsto ( \{ x_{0} + \alpha t \},\{ y_{0} + \beta t \} )\]Tale mappa rappresenta un moto di natura continua sul Toroide, con velocità:
\[\overrightarrow{v} = (\alpha,\beta)\]Per semplicità si scrive:
\[{\phi}_{1}(t) = \{ x_{0} + \alpha t \}\] \[{\phi}_{2}(t) = \{ y_{0} + \beta t \}\] \[\ \ \ \ \ \ \ \phi(t) = ( \phi_{1}(t),\phi_{2}(t) )\]Teorema 3
\(\phi\) è periodica \(\Leftrightarrow \frac{\alpha}{\beta}\mathbb{\in Q}\).
DIM: Supponiamo \(\phi\) sia periodica con periodo \(t>0\), allora:
Se \(\phi(t) = ( x_{0},y_{0} )\), cioè \({\phi}_{1}(t) = x_{0}\) e \({ \phi}_{2}(t) = y_{0}\).
Dalla prima si ha che:
\[\{ x_{0} + \alpha t \} = x_{0}\] \[x_{0} + \alpha t - \lbrack x_{0} + \alpha t \rbrack = x_{0}\] \[t = \frac{\lbrack x_{0} + \alpha t \rbrack}{\alpha}\]Dalla seconda si ha che: \(\{ y_{0} + \beta t \} = y_{0}\)
\[y_{0} + \beta t - \lbrack y_{0} + \beta t \rbrack = y_{0}\] \[t = \frac{\lbrack y_{0} + \beta t \rbrack}{\beta}\]Essendo che la \(t\) è la stessa in entrambi i casi, si possono eguagliare le equazioni:
\[t = \frac{n}{\alpha} = \frac{m}{\beta}\] \[\frac{\alpha}{\beta} = \frac{n}{m}\mathbb{\ \in Q}.\]D’altra parte, se \(\frac{\alpha}{\beta} = \frac{n}{m}\) con \(n,m\mathbb{\in N, n \neq 0 }\) si ha:
\[\phi(t) = ( \{ x_{0} + n \},\{ y_{0} + \frac{n\beta}{\alpha} \} )\]\(= ( \{ x_{0} + n \},\{ y_{0} + m\} = ( x_{0},y_{0} )\) per ogni \(n,m\mathbb{\in Z \smallsetminus}\{ 0 \}.\)
Teorema 4
L’immagine di \(\phi\) riempie densamente \(\lbrack 0,1)^{2} \Leftrightarrow \frac{\alpha}{\beta}\mathbb{\in R \smallsetminus Q}\).
DIM: Sia \(\frac{\alpha}{\beta}\mathbb{\in R \smallsetminus Q}.\) Sia \(( x_{1},y_{1} ) \in \lbrack 0,1)^{2}\), essendo \(\beta > 0\) si trova un tempo \(t_{0}\) tale che \({\phi}_{2}( t_{0} ) = y_{1}.\)
Allora si avrà che
\(\phi_{2}( t_{0} + \frac{n}{\beta} ) = \{ y_{0} + \beta t_{0} + n \} = \{ y_{0} + \beta t_{0} \} = {\phi_{2}( t_{0} ) = y}_{1}\) per ogni \(n\mathbb{\in Z}.\)
In altre parole, ad intervalli di tempo \(\frac{1}{\beta}\) la traiettoria della pallina interseca la retta \(y = y_{1}\).
Considerando la coordinata \(\phi_{1}( t_{0} )\) al tempo \(\frac{n}{\beta}\) , si ha che:
\[{\phi}_{1}( t_{0} + \frac{n}{\beta} ) = \{ x_{0} + \alpha t_{0} + {n \cdot \ }_{\overline{\beta}}^{\alpha} \} = T_{\frac{\alpha}{\beta}}^{n}( x_{0} + \alpha t_{0} ).\]Dal Teorema 2 sappiamo che \(\{ T_{\frac{\alpha}{\beta}}^{n}( x_{0} + \alpha t_{0} ) \}_{n}\) è densa in \(\lbrack 0,1)\) se \(\frac{\alpha}{\beta}\mathbb{\in R \smallsetminus Q}\).
Se ne conclude che:
\[\mathbb{N} \ni n \mapsto \phi( t_{0} + \frac{n}{\alpha} ) \in \lbrack 0,1)^{2}.\]Riempie densamente il segmento \(( x,y_{1} )\) con \(x \in \lbrack 0,1).\)
Ma allora \(t \mapsto \phi(t)\) si avvicina quanto si vuole anche a \(( x_{1},y_{1} )\).
Relazione tra Biliardo e Intervallo
Sulla base dei precedenti teoremi è possibile ora mettere in relazione \(\frac{\alpha}{\beta}\) del caso tridimensionale, con il passo \(\theta\) del caso unidimensionale.
Si ricorda che la traiettoria della pallina viene definita impostando una determinata pendenza, e che se non ci fosse alcuna parete si avrebbe una retta. Le limitazioni del calcolatore trattano tale retta come un grande segmento, in particolare tale segmento rappresenta l’ipotenusa di un triangolo rettangolo. Il passo \(\theta\) del caso unidimensionale può essere calcolato considerando la proiezione dell’ipotenusa di lunghezza \(l\) sull’asse delle ascisse.
\[\theta = l\cos\gamma\]Dove \(\gamma\) è l’angolo che la retta forma con l’asse delle ascisse.
Per quanto riguarda la pendenza, si ricorda che:
\[\overrightarrow{v} = (\alpha,\beta).\]Per cui se si considera l’equazione della traiettoria si deduce che:
\[f^{'}(x) = \frac{\alpha}{\beta}.\]Un’ulteriore conferma di ciò si può ricavare dal Teorema 4: ad intervalli di tempo \(\frac{1}{\beta}\) la traiettoria della pallina interseca la retta \(y = y_{1}\). Dunque si può ricavare \(\beta\) come:
\[\beta = \frac{1}{\theta}.\]Infine \(\alpha\) può essere ricavato in due modi differenti: considerando il reciproco della proiezione dell’ipotenusa sull’asse delle ordinate, oppure considerando che \(\frac{\alpha}{\beta} = \theta\).
Simulazioni
Di seguito si riporta una simulazione relativa al caso di moto periodico.

Il moto periodico produce una linea chiusa sul Toroide. Il punto di spawn della pallina è (0.2,0.4), mentre la pendenza è 0.2.
Si riportano inoltre i valori che caratterizzano tale simulazione.
| Intersezione | m | α | β | θ |
|---|---|---|---|---|
| (0.2, 0.4) | 0.2 | 1 | 0.2 | 5.0 |
| (0.2, 0.4) | 0.2 | 1 | 0.2 | 5.0 |
| (0.2, 0.4) | 0.2 | 1 | 0.2 | 5.0 |
| (0.2, 0.4) | 0.2 | 1 | 0.2 | 5.0 |
| (0.2, 0.4) | 0.2 | 1 | 0.2 | 5.0 |
| (0.2, 0.4) | 0.2 | 1 | 0.2 | 5.0 |
Di seguito si riporta una simulazione relativa al caso di moto non periodico.
Il moto non periodico riempie densamente il Toroide. Il punto di spawn della pallina è (0.2,0.4), mentre la pendenza è π.
Si riportano inoltre alcuni valori che caratterizzano tale simulazione.
| Intersezione | m | α | β | θ |
|---|---|---|---|---|
| (0.882, 0.4) | \(\pi\) | 1 | \(\pi\) | 0.31830988618379086 |
| (0.563, 0.4) | \(\pi\) | 1 | \(\pi\) | 0.31830988618379086 |
| (0.245, 0.4) | \(\pi\) | 1 | \(\pi\) | 0.31830988618379086 |
| (0.927, 0.4) | \(\pi\) | 1 | \(\pi\) | 0.31830988618379086 |
| (0.608, 0.4) | \(\pi\) | 1 | \(\pi\) | 0.31830988618379086 |
| (0.290, 0.4) | \(\pi\) | 1 | \(\pi\) | 0.31830988618379086 |
Riferimenti bibliografici
| Fonti Utilizzate |
|---|
| Appunti presi durante le lezioni di Analisi I tenute dal Professore Matteo Dalla Riva |
| L. Menini, C. Possieri and A. Tornambè (2020). “Trajectory tracking in rectangular billiards” |